Teoria delle reti
La teoria delle reti studia caratteristiche e comportamenti delle reti complesse, che anche se riguardano gli argomenti più diversi, hanno strutture e dinamiche determinati non dal genere di rete, ma dall’essere una rete. Proprietà comuni si ritrovano in reti tecnologiche come Internet o il Web, biologiche come i sistemi metabolici, proteici, epidemiologici, reti sociali come le comunità scientifiche, i dipendenti di grandi aziende, studenti e professori di una università.
Le strutture organizzative di una rete vanno dal reticolo regolare all’insieme caotico, passando per le reti scale-free e i piccoli mondi. Attraverso i loro collegamenti, i nodi di una rete possono scambiarsi informazioni simboliche e virtuali (internet), merci e persone (ferrovie, linee aeree), risorse (materie prime e semilavorati), malattie (AIDS), attentati terroristici o azioni mafiose.

La teoria delle reti fa parte della teoria dei grafi, una branca della matematica che permette di descrivere insiemi di oggetti con le loro relazioni. Un grafo è un struttura in cui due nodi sono uniti da un arco. I nodi possono essere individui e oggetti concreti o entità astratte, gli archi possono indicare relazioni, appartenenze, azioni. Due o più grafi costituiscono una rete, che può andare da un gruppo di amici che si vedono per giocare a carte, fino ai miliardi di attori che si collegano nel web. I grafi sono dunque gli elementi essenziali di una rete, e come tali forniscono un linguaggio unificante per descrivere la struttura di una rete.
La possibilità di raccogliere dati su larga scala usando computer e reti di computer consente di individuare e misurare proprietà statistiche che caratterizzano la struttura delle reti, creare modelli di reti, descriverne e prevederne la formazione e i comportamenti. Lo sviluppo tecnologico e la capacità di gestire quantità sempre crescenti di dati ha generato reti più grandi e complesse, costituite da milioni di unità comunicanti fra loro.
I metodi matematici basati sulla teoria dei grafi vengono impiegati per estrarre le informazioni dalle reti complesse in maniera sintetica ed oggettiva, modellizzando aspetti che non si possono vedere a occhio nudo. I modelli scale-free (SF) e small-world (SW) riflettono adeguatamente le proprietà delle reti complesse reali, indipendentemente dalla natura della rete considerata. Le misure basate sulla teoria dei grafi (grado, distribuzione, efficienza) descrivono le proprietà dei modelli e del modo in cui si organizzano all’interno della rete di cui fanno parte.
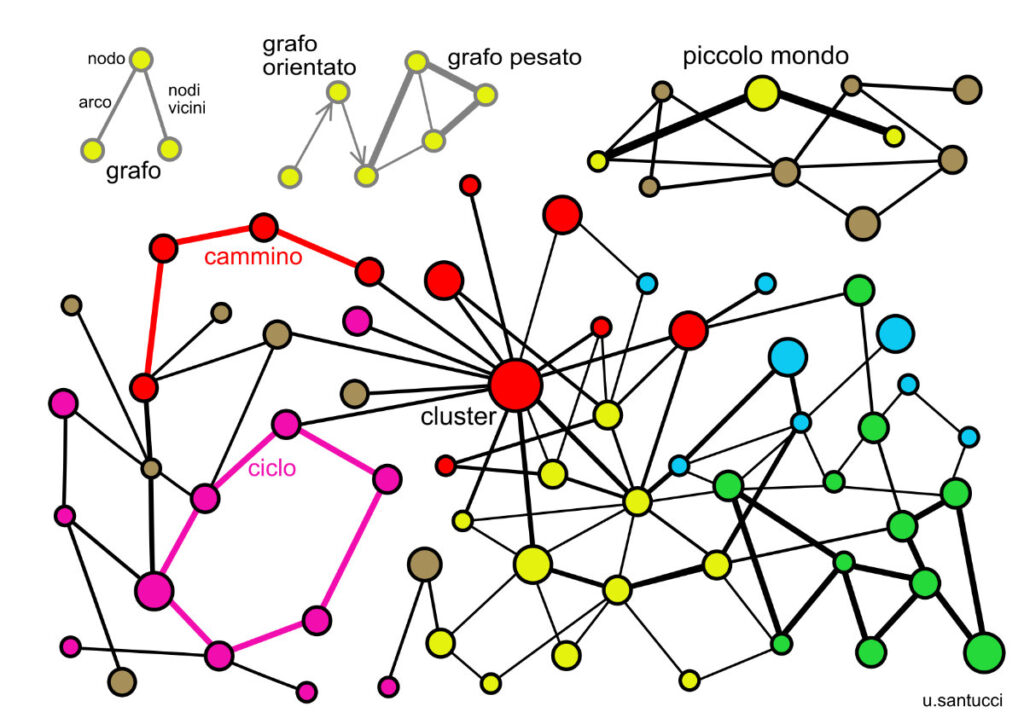
Un grafo è un insieme di nodi (vertici) e di archi (collegamenti). Due nodi sono vicini se sono collegati da un arco. Gli archi possono rappresentare il semplice collegamento o anche la sua direzione (grafo orientato) e il suo peso (grafo pesato).
Il cammino è la sequenza di nodi e archi che vanno verso un estremo.
Il ciclo è un percorso che inizia e termina con lo stesso nodo. Un nodo può far parte di più cicli.
La connettività descrive le connessioni di un grafo, che si dice connesso se da ogni nodo si può raggiungere un altro nodo.
Le componenti sono nodi e sottoinsiemi connessi o non connessi. Le componenti giganti sono grossi cluster o grossi hub; in genere in una rete ce n’è una sola e la caratterizza.
La distanza fra due nodi è il percorso minimo che li unisce (Linkedin, contatti di 1° e 2° livello); l’intorno è l’insieme dei nodi vicini, anche se non connessi.
Il piccolo mondo è la distanza minima fra due nodi, e in genere non supera i sei gradi di separazione, indipendentemente dalle dimensioni della rete.

Una rete scale-free o a invarianza di scala è una rete costituita di nodi e link che si aggregano in modo simile e indipendente dalla loro quantità. Questa proprietà è ben rappresentata da un frattale.
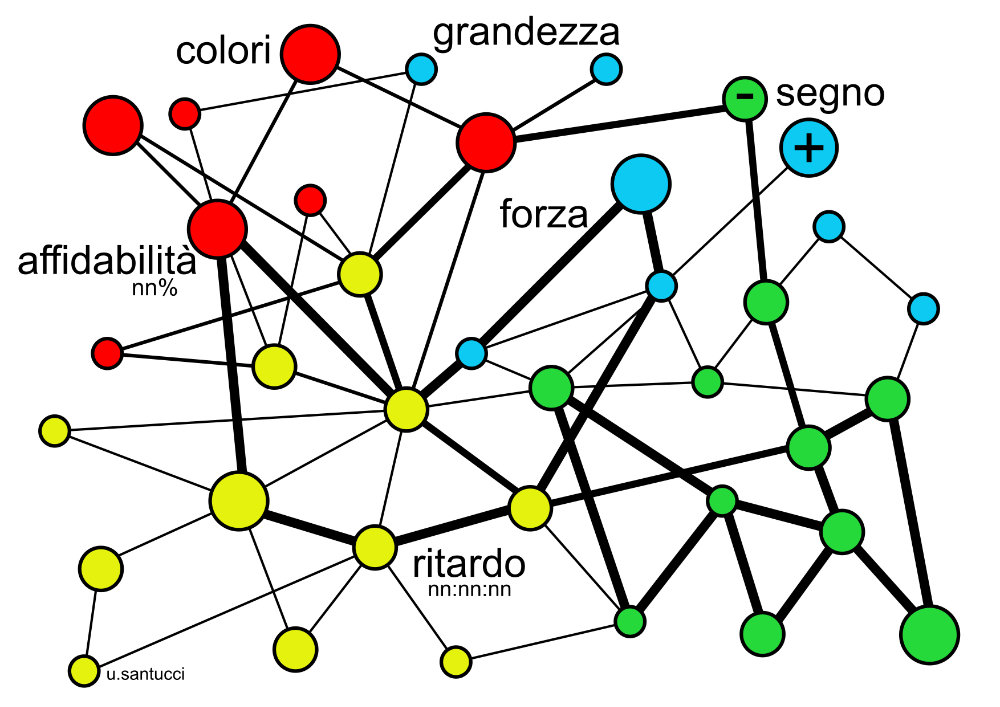
Gli archi possono avere informazioni aggiuntive. Il segno distingue fra amici e nemici, la forza è l’intensità della relazione fra i nodi, il ritardo è il tempo di trasmissione, l’affidabilità è la percentuale di errore nella trasmissione di dati fra un nodo e l’altro. I colori possono rappresentare altri tipi di informazioni, e la grandezza dei nodi la loro importanza quantitativa, come accade nel diagramma di Venn.

